Lokale Änderungsrate
Ziel:
Bestimmung des Tangentenanstiegs
mittl. Änderungsrate → lokale Änderungsrate
Tangentenanstieg ist der Grenzwert der Folge der Sekantenanstiege
Def.:
Es sei f eine Funktion, die in einer Umgebung von x0 definiert ist.
f ist an der Stelle x0 differenzierbar dann, wenn der Grenzwert 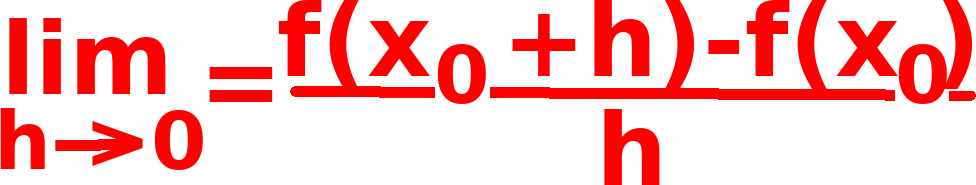 existiert.
existiert.
Satz:
Die Ableitungsfunktion f'(x) ordnet jeder Stelle x ihrem Tangentenanstieg zu. mt = f'(x)
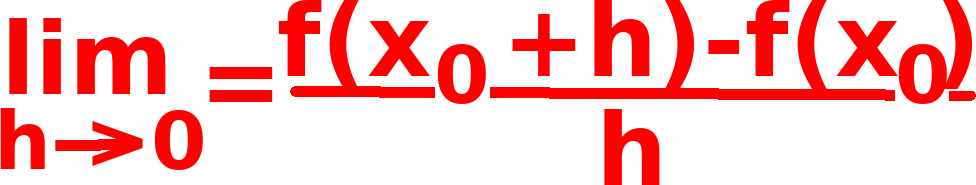 existiert.
existiert.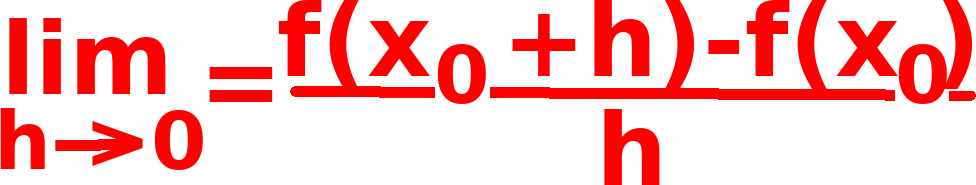 existiert.
existiert.