Kurvendiskussion
Funktion: f(x)=2x³-6x²
Funktion: f(x)=2x³-6x²
|
Schnittpunkte mit den Koordinatenachsen
y-Achse: f(x)=0
x-Achse: x=0
|
Aufgabe:
0=2xn³-6xn²
0=xn²×(2xn-6)
Lösung:
→ x1,2 = 0 → x3 = 3
x=0
Lösung:
Sy(0/0) |
|
Symmetrie
ist f(x)=f(-x) ?
ist f(x)=-f(-x) ?
|
Aufgabe:
f(-x)=-2x³-6x²
Lösung:
≠ f(x)
-f(-x)=2x³+6x²
Lösung:
→ weder gerade noch ungerade
≠ f(x) |
| Ableitungen |
f'(x)= 6x²-12x
f''(x)= 12x-12
f'''(x)= 12
|
| Extrema → notwendige Bed.: f'(xE)=0 → hinreichende Bed.: f''(xE)≠0 (Position der Punkte) |
Aufgabe:
0=6xE²-12xE
0=xE×(6xE-12)
Lösung:
→ xE1=0 → xE2=2
Lösung:
f''(0)=-12 → Maximalstelle f''(2)=12 → Minimalstelle
f(0)=0
f(2)=-8
Lösung:
H(0/0) T(2/-8) |
| Wendepunkte → notwendige Bed.: f''(xW)=0 → hinreichende Bed.: f'''(xW)≠0 (Position der Wendepunkte) |
Aufgabe:
0=12xW-12
Lösung:
→ xW=1
Lösung:
f(1)=12 ≠ 0 → R-L
f(1)=-4
Lösung:
→ W(1/-4) |
| Wendetengente
f'(x)=m y=mx+n |
Aufgabe:
f'(1)= -6
m= -6 -4=-6×1+n n=2
Lösung:
t(x)=-6x+2 |
| Graph |
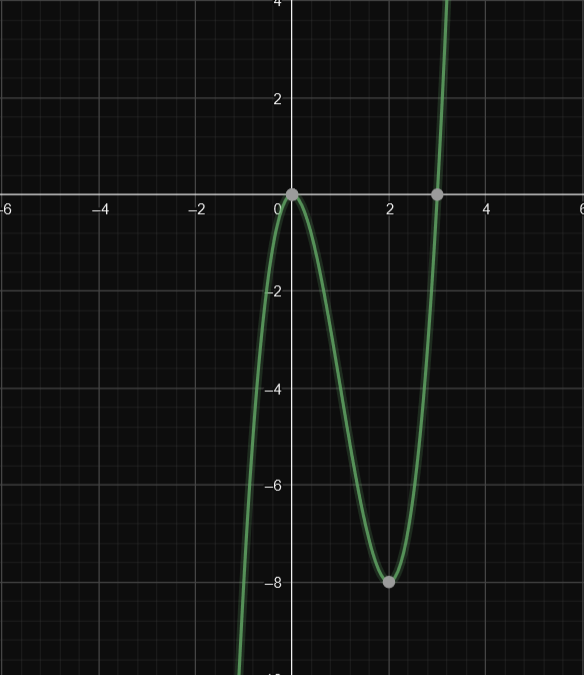
|
| Monotonie |
Lösung:
-∞ < x < 0 → monoton steigend 0 < x < 2 → monoton fallend 2 < x < ∞ → monoton steigend |
| Verhalten im Unendlichen |
Lösung:
lim f(x)= ∞ x→∞ lim f(x)= -∞ x→-∞ |